BUILDING A CHAMFERBOX
To achive this correctly in 3D, it is important that the data meet some requirements. First, the vertices must be unique. Without this translating verts would form cracks and gaps. An example of this can be found here: http://deltronslair.com/gridmonster.zip
The way we will split and extend the vertices is to create a plane, translating all vertices on one side of the plane in one direction, and all vertices on the other side of the plane in the opposite direction. Then we just repeat the process for the remaining two axis planes.
To define a plane we need a point P, and a unit normal n. Given this information, a plane will be defined perpendicular to the unit normal, with the point P on this plane.
The standard equation of a plane is:

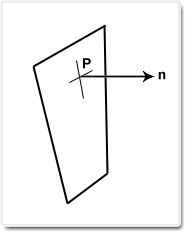
Ax + By + Cz + D = 0

Where (A,B,C) is the unit normal, and (x,y,z) is a point on the plane.

To solve for D we rewrite the equation as:

D = -(Ax + By + Cz)
Now, I will deliberately choose my point to always be located at the origin and have my data standardized around this origin. This will make things very easy.

So my point (x,y,z) equals (0,0,0)

Substituting we have:

D = -(A*0 + B*0 + C*0)

So,  D = 0

For any given vertex (Vx,Vy,Vz) the equation becomes:

Side = AVx + BVy + CVz + D

If Side is greater than zero, then the vertex lies on the same side as the normal.

If Side is less than zero, then the vertex lies on the other side of the normal.

If Size is zero, then the vertex lies on the plane.

So to define the three planes along each axis we have:

(A,B,C) = (1,0,0)
(A,B,C) = (0,1,0)
(A,B,C) = (0,0,1)

To test a given vertex (Vx,Vy,Vz) against our first plane we have:

Side = 1*Vx + 0*Vy + 0*Vz + 0

Simplifying we have:

Side = Vx

Ta da!
The pseudo code would be:

const float chamfsize = 1.0f;
for every defined vertex in my data
If the Vx component is > 0, add chamfsize to it
If the Vx component is < 0, subtract chamfsize from it

At this point the object will resemble a pill or capsule shape.

An example can he found here: http://deltronslair.com/capsule.zip